If you ever flew in a plane, you probably realized that the plane took a curved path instead of a straight path (if you were looking at a flat map). This is because on a sphere, the shortest distance between two points is along a great circle. This is more obvious when you plot the straight and curved paths on a flat map (which uses the Mercator projection) and on a sphere.
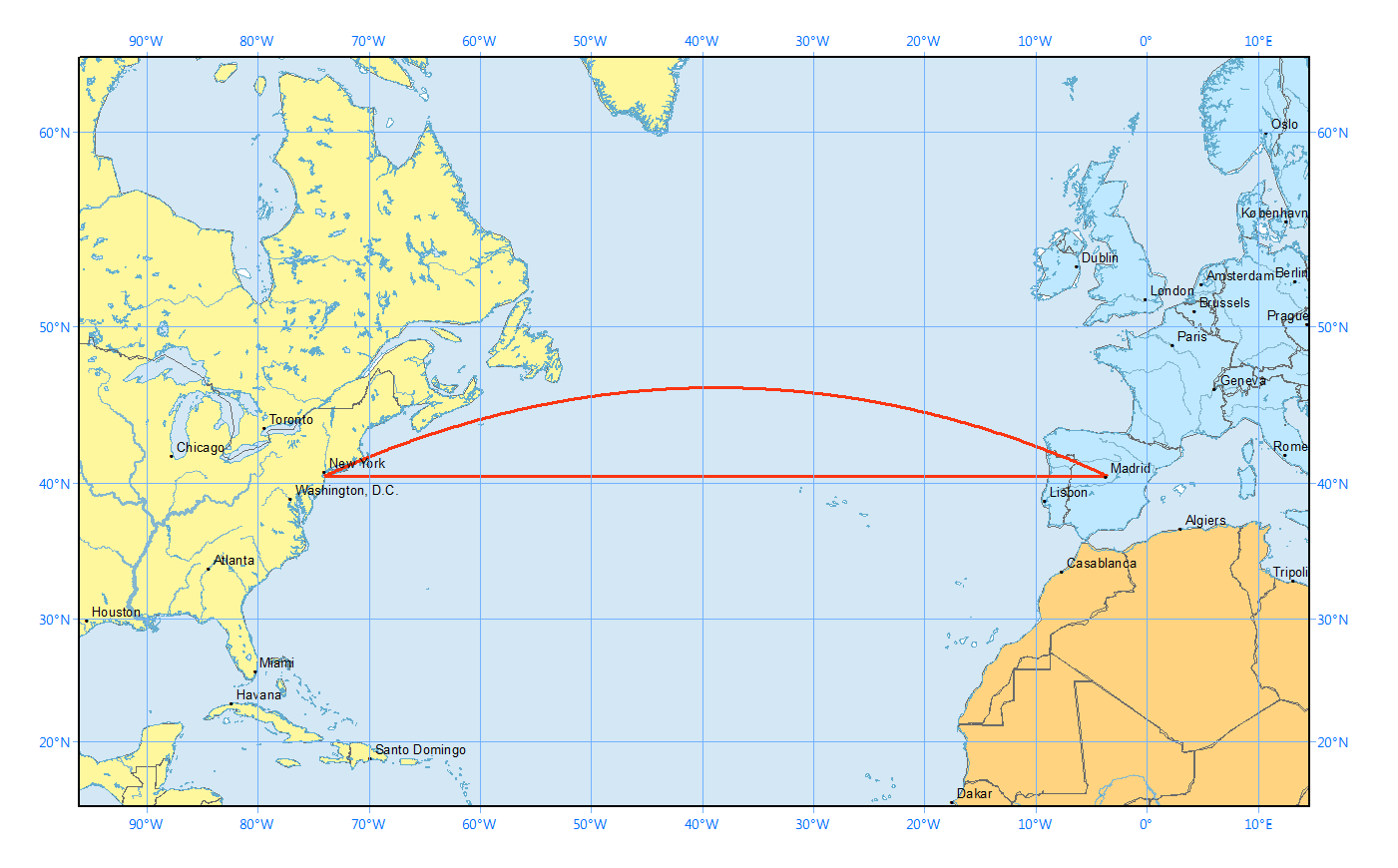
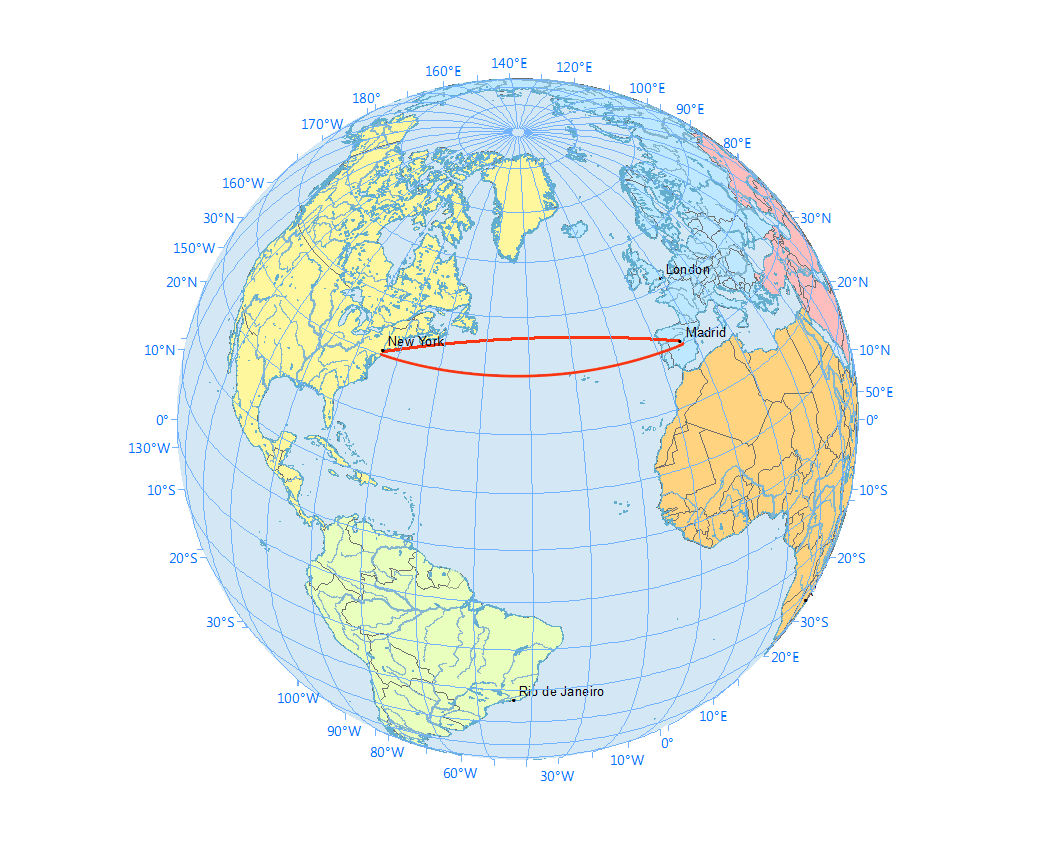
You can calculate the length of the curved path using the haversine formula. Between two points on the Earth $(\phi_1, \lambda_1)$ and $(\phi_2, \lambda_2)$ where $\phi$ is latitude and $\lambda$ is longitude, the shortest distance is $$ 2R \arcsin \sqrt{ \sin^2 \left( \frac{\phi_2 - \phi_1}{2} \right) + \cos\phi_1 \cos\phi_2 \sin^2 \left( \frac{\lambda_2 - \lambda_1}{2} \right)} $$ where $R$ = 6372.1 km is the radius of the Earth.
Input: (Latitude, longitude) coordinates of two points. Latitudes go from -90 to +90. Longitudes go from -180 to +180. Remember to convert your angles from degrees to radians before using the sine and cosine functions!
Output: The distance between the points in kilometers (km).
Example
| Difficulty | Timesink | ||
|---|---|---|---|
| Function | haversine_distance(lat1, lon1, lat2, lon2) | ||
You must be logged in to view your submissions.
Let us know what you think about this problem! Was it too hard? Difficult to understand? Also feel free to discuss the problem, ask questions, and post cool stuff on Discourse. You should be able see a discussion thread below. Would be nice if you don't post solutions in there but if you do then please organize and document your code well so others can learn from it.