Welcome to Project Lovelace! We're still in early development so there are still tons of bugs to find and improvements to make.
If you have any suggestions, complaints, or comments please let us know on Discourse, Discord, or GitHub!
The simple problem here is to sum the area of a bunch of rectangles with different heights but the same width. That's
all you need to know. But if you don't mind learning a bit of calculus, read on.
The slightly longer version is that we're trying to calculate the area under a complicated line or curve (the black
line in the figure below). One way to do this is to draw rectangles under the curve and just add up the areas of all
these rectangles. You can choose the rectangles in a few different ways but the idea is that if you use more and more
rectangles, you'll get a more accurate answer (see figure caption).
If the black curve is described by a function $f(x)$ then the area under the curve is the definite integral of $f$
between some endpoints $a$ and $b$
$$ \int_a^b f(x) \, dx \approx \sum_{k=0}^N f(x_i) \Delta x $$
where we decided to use $N$ rectangles each of width $\Delta x$. The height of the $i^\textrm{th}$ rectangle is
$f(x_i)$ which can be chosen in a few different ways but is given in this problem.
You can choose the rectangles in a bunch of different ways. The height of the
green rectangles was chosen to be the maximum value of the function over the
width of the rectangle while the red rectangles use the minimum value of the
function. The blue rectangles use the value at the left endpoint (where the
rectangle starts) while the yellow rectangles use the right endpoint (where
the rectangle ends). But if you use more and more rectangles, you get a more accurate answer and the are calculated
by the four methods all converge to the same number (inset).
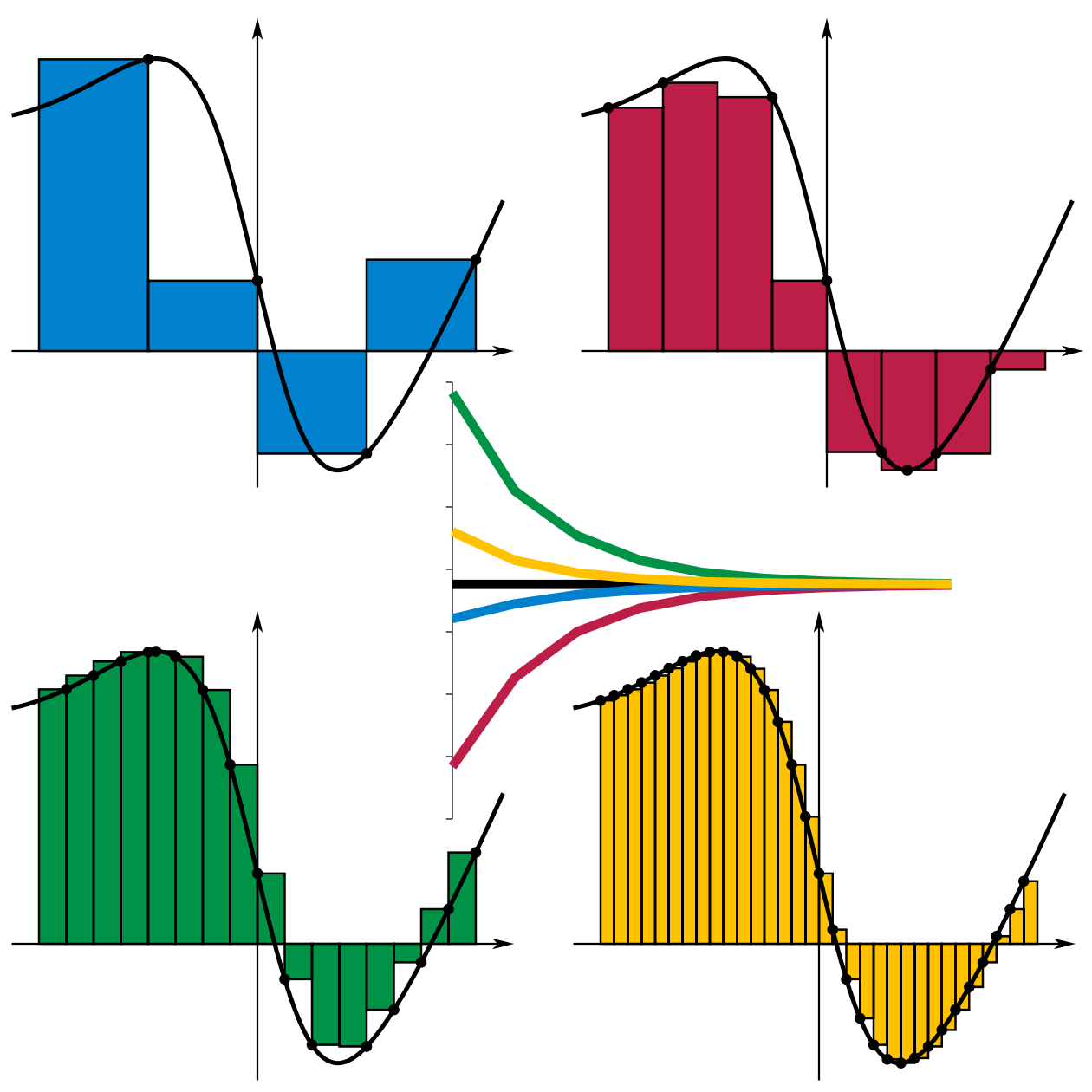
Input:
A list of rectangle heights (negative heights give a rectangle "negative area"), and a rectangle width.
Output:
The sum of the rectangle areas.
Example 1
Input list of rectangles: [0, 1, 2, 3, 4, 5]
Input rectangle width: 1.5
Output area: 22.5
Example 2
Input list of rectangles: [-1, 2, -3, 4, -5]
Input rectangle width: 2
Output area: -6
The method we used to compute the area under the curve here using rectangles is called a
Riemann summation. You could use more complicated shapes:
The trapezoidal rule uses trapezoids and
Simpson's rule uses quadratic polynomials.
Instead of using upright rectangles like we did here with the Riemann sum, you can use rectangles placed sideways
which is kind of how the area under the curve is interpreted with
Lebesgue integration.
Let us know what you think about this problem! Was it too hard? Difficult to understand? Also feel free to
discuss the problem, ask questions, and post cool stuff on Discourse. You should be able see a discussion
thread below. Would be nice if you don't post solutions in there but if you do then please organize and
document your code well so others can learn from it.
