Correlation does not imply causation

Two variables are correlated if there's some statistical relationship between the two. However, just because two variables are correlated does not mean that one is caused by the other. This misconception is commonly referred to as “correlation does not imply causation”.

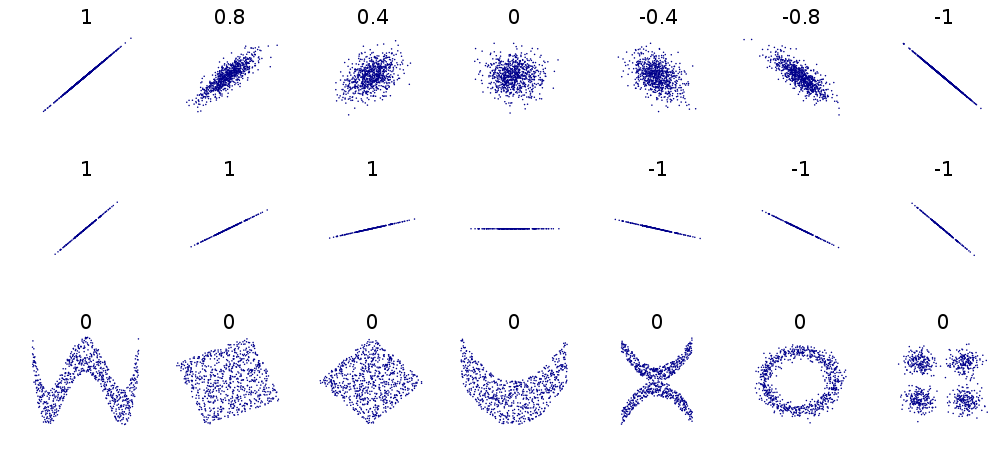
One way of computing a correlation coefficient between two variables $X$ and $Y$ with $n$ measurements $x_1, x_2, \dots, x_n$ and $y_1, y_2, \dots, y_n$ is the Pearson correlation coefficient $$ r = \frac{\operatorname{cov}(X,Y)}{\sigma_X\sigma_Y} $$ where $$ \operatorname{cov}(X,Y) = \frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})(y_i - \overline{y}) = \frac{1}{n} \left[ (x_1-\overline{x})(y_1-\overline{y}) + \cdots + (x_n-\overline{x})(y_n-\overline{y}) \right] $$ is the covariance between $X$ and $Y$, \begin{align} \sigma_X & = \sqrt{\frac{1}{n} \sum_{i=1}^n (x_i - \overline{x})^2} = \sqrt{\frac{1}{n} \left[ (x_1 - \overline{x})^2 + \cdots + (x_n-\overline{x})^2 \right]} \quad \text{and} \\ \sigma_Y & = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - \overline{y})^2} = \sqrt{\frac{1}{n} \left[ (y_1 - \overline{y})^2 + \cdots + (y_n-\overline{y})^2 \right]} \end{align} are the standard deviations of $X$ and $Y$, and $$ \overline{x} = \frac{1}{n} \sum_{i=1}^n x_i = \frac{x_1 + x_2 + \cdots + x_n}{n} \quad \text{and} \quad \overline{y} = \frac{1}{n} \sum_{i=1}^n y_i = \frac{y_1 + y_2 + \cdots + y_n}{n} $$ are the averages (or means) of the $X$ and $Y$ measurements. The Pearson correlation coefficient $r$ is always between -1 and 1.

Taking in two lists of measurements $x_n$ and $y_n$, return the Pearson correlation coefficient for them.

Input: Two lists $x_n$ and $y_n$ of size $n$.

Output: The Pearson correlation coefficient $r$ between the two variables.