Example 1
Input n: 8
Output numerator: -1
Output denominator: 30
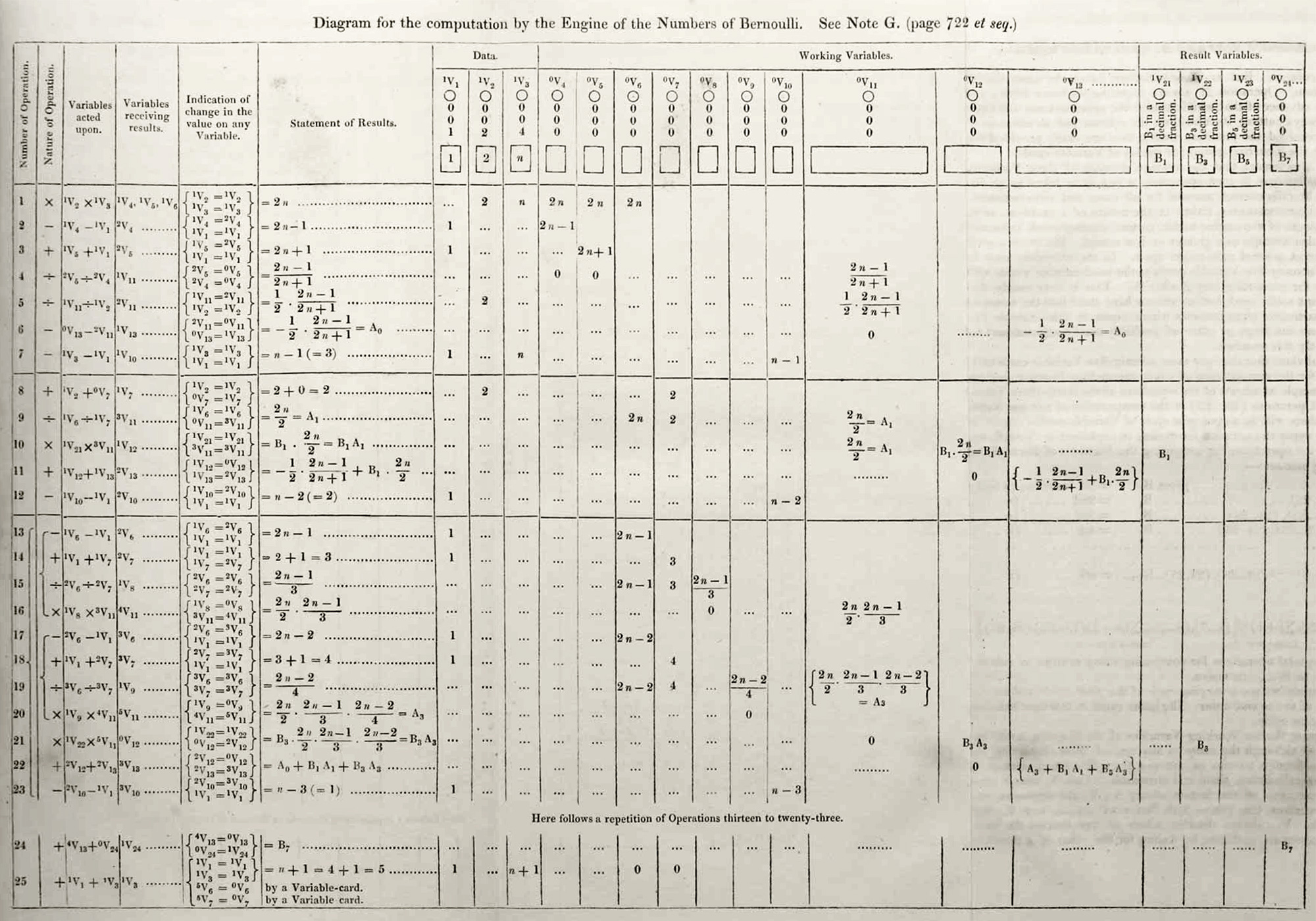
Ada Lovelace (1815-1852) was an English mathematician who was the first person to realize that computers could be much more than big calculators and published the first complex computer algorithm in 1843. She did this long before any computer existed to execute her algorithm as it was devised for the Analytical Engine which never got built. The algorithm, detailed in Note G of Sketch of The Analytical Engine Invented by Charles Babbage by Luigi Menabrea with notes by Ada Lovelace described how the Analytical Engine could calculate the Bernoulli numbers using a recursive algorithm, which you will reproduce here.
The Bernoulli numbers $B_n$ are a sequence of rational numbers (fractions) that tend to show up in many places in mathematics, and there are many ways of calculating them. One method is to calculate them recursively where calculating $B_n$ involves knowing $B_0, B_1, \dots, B_{n-1}$. A derivation of how Ada Lovelace came up with the formula is posted in the notes tab, but she essentially used the following formula $$ B_n = -\sum_{k=0}^{n-1} \frac{n!}{(n+1-k)!\cdot k!} B_k = -\sum_{k=0}^{n-1} \binom{n}{k} \frac{B_k}{n+1-k} $$ where $B_n$ is calculated from $B_0, B_1, \dots, B_{n-1}$. Here $\displaystyle \binom{n}{k} = \frac{n!}{k!(n-k)!}$ is a binomial coefficient, and $n! = n(n-1)(n-2)\cdots3\cdot2\cdot1$ is the factorial which is the product of all positive integers less than or equal to $n$. $B_0 = 1$ while there are two choices for $B_1$ corresponding to two conventions and we will choose $\displaystyle B_1 = -\frac{1}{2}$ which most modern textbooks use.
Write a function that calculates $B_n$ and returns the numerator and denominator. If $B_n$ is negative, the minus sign should be included with the numerator.
Input: An integer $n$.
Output: The numerator and denominator of the $n^\textrm{th}$ Bernoulli number $B_n$. If $B_n$ is negative, the minus sign should be included with the numerator. If $B_n = 0$ then return a numerator of 0 and a denominator of 1.
| Difficulty | Timesink | ||
|---|---|---|---|
| Function | bernoulli(n) | ||
You must be logged in to view your submissions.
To see how Ada derived her formula for the Bernoulli numbers we will have to make use of the fact that $e^t$ can be expressed as an infinite series $\displaystyle e^t = \sum_{n=0}^\infty \frac{t^n}{n!:}$ which is called its Taylor series. The Bernoulli numbers $B_n$ can be defined as the coefficients of the Taylor series of a generating function $$ \frac{t}{e^t - 1} = \sum_{n=0}^\infty B_n \frac{t^n}{n!} $$ We now want to solve for $B_n$ to get a formula for the Bernoulli numbers we can use to program a computer. We move both terms to a single side and insert the Taylor series for $e^t$ to get $$ 1 = \frac{e^t - 1}{t} \sum_{n=0}^\infty B_n \frac{t^n}{n!} = \sum_{m=0}^\infty \frac{x^m}{(m+1)!} \sum_{n=0}^\infty B_n \frac{t^n}{n!} $$ We now have the product of two infinite series so let's expand their product up to terms including $t^4$. This gives us \begin{align*} 1 &= \left( 1 + \frac{t}{2} + \frac{t^2}{2\cdot3} + \frac{t^3}{2\cdot3\cdot4} + \frac{t^4}{2\cdot3\cdot4\cdot5} + \mathcal{O}(t^5) \right) \left( B_0 + B_1t + B_2 \frac{t^2}{2} + B_3\frac{t^3}{2\cdot3} + B_4\frac{t^4}{2\cdot3\cdot4} + \mathcal{O}(t^5) \right) \\ &= B_0 + \left( B_1 + \frac{B_0}{2} \right) t + \left( \frac{B_2}{2} + \frac{B_1}{2} + \frac{B_0}{2\cdot3} \right)t^2 + \left( \frac{B_3}{2\cdot3} + \frac{B_2}{2\cdot2} + \frac{B_1}{2\cdot3} + \frac{B_0}{2\cdot3\cdot4} \right) t^3 \\ & \quad + \left( \frac{B_4}{2\cdot3\cdot4} + \frac{B_3}{2\cdot2\cdot3} + \frac{B_2}{2\cdot2\cdot3} + \frac{B_1}{2\cdot3\cdot4} + \frac{B_0}{2\cdot3\cdot4\cdot5} \right) t^4 + \mathcal{O}(t^5) \end{align*} where we grouped terms with the same powers of $t$. Now we can start calculating the Bernoulli numbers. The left and right hand sides must be equal so $B_0 = 1$. As $t$ does not appear on the left, we can calculate $B_1$ using $$ B_1 + \frac{B_0}{2} = 0 \quad \implies \quad B_1 = -\frac{B_0}{2} = -\frac{1}{2} $$ and similarly for $B_2$ as $t^2$ does not appear on the left $$ \frac{B_2}{2} + \frac{B_1}{2} + \frac{B_0}{2\cdot3} \quad \implies \quad B_2 = -2\left( \frac{B_1}{2} + \frac{B_0}{6} \right) = -2\left( -\frac{1}{4} + \frac{1}{6} \right) = \frac{1}{6} $$ Repeating the process for the $t^3$ and $t^4$ terms we find $B_3 = 0$ and $\displaystyle B_4 = -\frac{1}{30}$. We also notice a pattern: the coefficient of $t^n$, which is equal to zero, is given by \begin{multline} 1\cdot\frac{B_n}{2\cdot3\cdot4\cdots(n+1)} + \frac{1}{2} \cdot \frac{B_{n-1}}{2\cdot3\cdot4\cdots n} + \frac{1}{2\cdot3} \cdot \frac{B_{n-2}}{2\cdot3\cdot4\cdots (n-1)} + \cdots \\ + \frac{1}{2\cdot3\cdots(n-2)} \cdot \frac{B_3}{2\cdot3} + \frac{1}{2\cdot3\cdots(n-1)} \cdot \frac{B_2}{2} + \frac{1}{2\cdot3\cdots n} \cdot B_1 + \frac{1}{2\cdot3\cdots(n+1)} \cdot B_0 = 0 \end{multline} which we can write as $$ \sum_{k=0}^n \frac{1}{(n+1-k)!} \cdot \frac{B_n}{k!} = 0 $$ and so if we take out the $B_n$ term we can express it in terms of $B_k$ for $k \lt n$ $$ B_n = -\sum_{k=0}^{n-1} \frac{n!}{(n+1-k)!\cdot k!} B_k = -\sum_{k=0}^{n-1} \binom{n}{k} \frac{B_k}{n+1-k} $$ Using this formula along with $B_0 = 1$ we can calculate any Bernoulli number $B_n$ as long as we know all the lower Bernoulli numbers $B_0, B_1, B_2, \dots, B_{n-1}$. In Ada Lovelace's Note G, she proposes an algorithm for calculating what we call $B_8$, which she labeled $B_7$.
Let us know what you think about this problem! Was it too hard? Difficult to understand? Also feel free to discuss the problem, ask questions, and post cool stuff on Discourse. You should be able see a discussion thread below. Would be nice if you don't post solutions in there but if you do then please organize and document your code well so others can learn from it.